费尔巴哈定理如下:九点圆和三角形的内切圆和旁切圆相切。那么几何画板怎么验证费尔巴哈定理呢?接下来小编就为大家带来解答,一起看看吧。
操作步骤如下:
步骤一 画出九点圆。
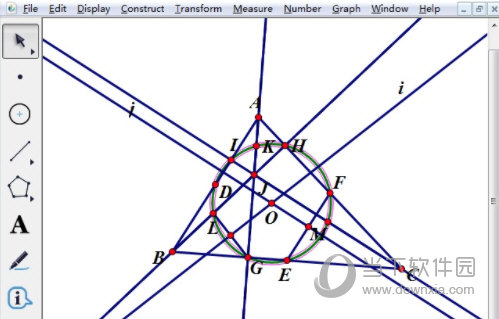
步骤二 作内切圆。选择点B、A、C,选择“构造”菜单中的“角平分线”,作出∠BAC 的平分线k, 用同样的方法作出∠ABC平分线l,选择角平分线k、l,选择“构造”菜单中的“交点”,作出内切圆圆心Q,选择点Q、线段BC,选择“构造”菜单中的“垂线”,作出线段BC的垂线m,求出线段BC和垂线m的交点R。 选择点Q、R,选择“构造”菜单中的“以圆心和圆周上的点作圆”,作出内切圆Q。
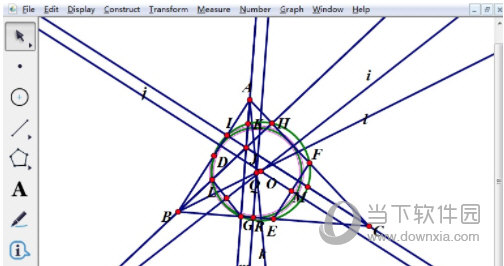
步骤三 作旁切圆。选择点B、A,选择“构造”菜单中的“直线”,在直线AB上取一点S,选择点C、A、S,选择“构造”菜单中的“角平分线”,作出∠CAS 的平分线n,选择角平分线l、n,选择“构造”菜单中的“交点”,作出旁切圆圆心T,选择点T和线段AC,选择“构造”菜单中的“垂线”,作出垂线,求出AC和垂线的交点U,选择点T、U,选择“构造”菜单中的“以圆心和圆周上的点作圆”,作出旁切圆T。
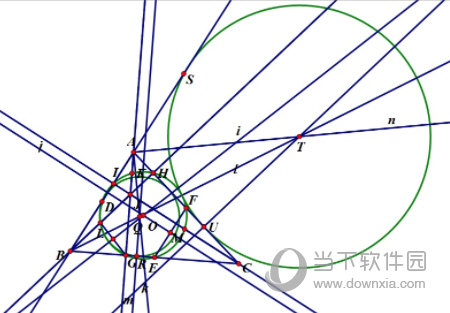
步骤四 隐藏辅助线,得到如下图所示的九点圆的内切圆和旁切圆。
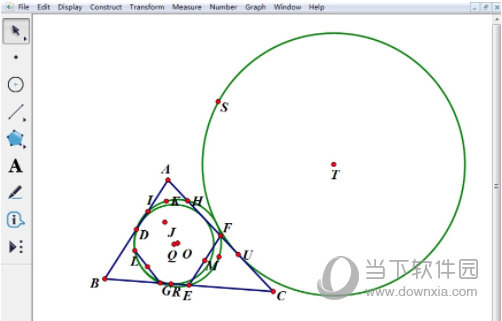
以上给大家讲解了画出九点圆的内切圆和旁切圆的方法,也由此验证了费尔巴哈定理的正确性。费尔巴哈定理描述了三角形的九点圆与其内切圆以及三个旁切圆的位置关系,是平面几何学中十分优美的定理之一。